距離減衰の考え方

音は距離が増すほど減衰します。

点音源の場合は倍距離 -6dB
線音源の場合は倍距離 -3dB

ところが、面音源の場合は距離による減衰はありません。　これは、距離減衰の考え方が、音のエネルギーの拡散によるものだからです。

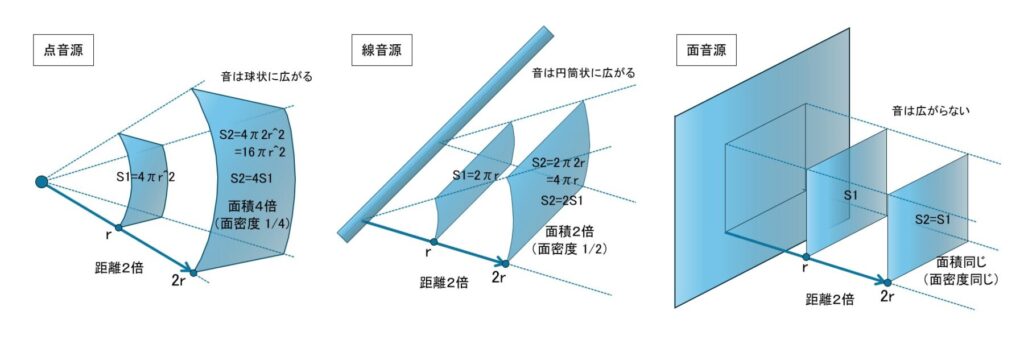
点音源を球体と考えると、球体の表面積は 4πr^2 で求められますから、半径が２倍になると面積は４倍になります。　これにより音のエネルギー密度が 1/4 になるため、デシベルで換算すると -6dB になります。

10*log(1/4)=-6.02

線音源の場合は、近似的に無限に長い円筒状表面積を 2πr として考えます。　距離が２倍になると表面積も２倍になる為、エネルギー密度は 1/2 になります。　これをデシベルで換算すると -3dB になります。

10*log(1/2)=-3.01

では面音源の場合はといいますと、表面積を無限に広い場合と仮定すると、音源から離れてもエネルギーの拡散はありません。　したがって、面音源は距離によって減衰しないと考えます。

ところが、現実的には球体の音源は見かけませんし、無限に長い線状の音源や、ましてや無限に広い面状の音源も存在しません。　では、どのように音源の状態を判断すればよいのでしょう。

現実的な距離減衰の計算方法

一般的な例として、音源の状態は次のように考えます。

点音源・・・音源の大きさに対して十分に離れた位置から見た音源。（飛行機やヘリコプター、自動車、エアコン室外機など）
線音源・・・線音源そのものや、点音源が線状に並んでいる場合。（風でうなる送電線、幹線道路の自動車走行音、鉄道の走行音など）
面音源・・・面音源そのものや、点音源が面状に並んでいる場合。（工場の外壁や、都市部の地表面に対し鉛直上向きの音の伝搬など）

ある程度離れた距離で考える場合は、上記の観点から音源の状態を判断します。　しかしながら、十分離れた位置では点音源と考えて問題なくても、距離が近くなると線音源か面音源かの判断が難しい場合があります。　このような場合は以下の図を参考に考えます。

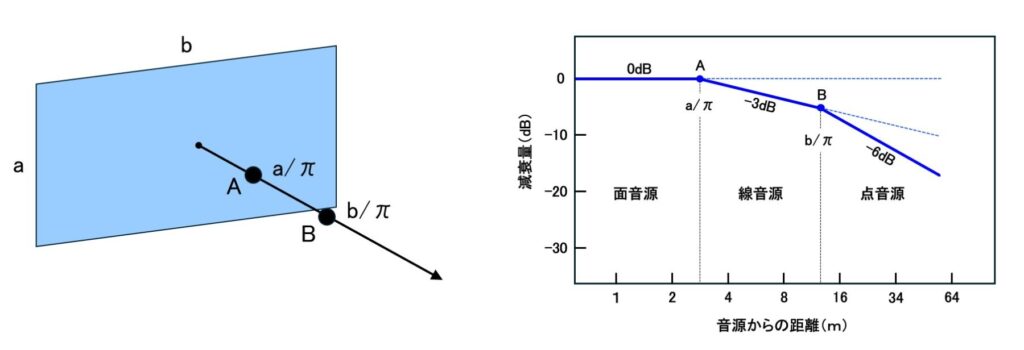
つまり、音源の短い辺の長さの 1/3 の距離までは面音源として考え、長い辺の長さの 1/3 までの距離は線音源として考えます。　それ以上の距離であれば点音源として考える事になります。

ここで注意しなければならないのは、測定した位置を基準として考える場合、その位置が上図のＢ点より音源に近い位置であれば、Ｂ点までは面音源あるいは線音源としての距離計算を行い、Ｂ点からは点音源の距離減衰計算を行う必要があります。

ただ、このよう複合した計算が必要になる場面は、工場など大きな面積を持った外壁面が音源となる場合か、鉄道騒音などの線音源を、離れた位置で評価する場合なので、一般的には短辺の 1/3 以内は面音源、長辺の 1/3 以内は線音源、それ以上は点音源として考えて問題ないと思います。

距離減衰計算と現実

音の距離減衰を示す物理計算式ですが、実際の環境は本当に計算通りの特性を示すのでしょうか。

この問いに対し、弊所では次のようなアプローチで計算の信頼性を確保しています。まず、対象エリアの3点以上で騒音の同時測定を行い、これを基準値とします。その上で、実測点の間を補完するために距離減衰計算を用いるのです。この手法により、計算のみに頼った場合の過小評価といったリスクを防ぎつつ、常に実測値との比較ができるため、計算結果そのものの信頼性を担保することができます。

長年にわたりこの手法を実践してきましたが、建物による反射や地形による回折といった要素を丁寧に考慮すれば、計算誤差はほとんどの場合で1dB以内に収まります。重要なのは、恣意的な調整定数を用いるのではなく、現場の状況を注意深く観察し、物理現象に忠実なモデルで計算することです。そうすれば、自ずと誤差の少ない結果が得られます。

このような精度の高い結果に触れるたび、物理計算がいかに現実に即した、信頼性の高いツールであるかを改めて実感させられます。

背景騒音の存在

音源から離れるにつれて伝搬する音のレベルは減少していきます。これが「距離減衰」の基本です。しかし、騒音は無限に小さくなるわけではなく、その場所にもともと存在する**背景騒音（暗騒音）**のレベルより小さくなることはありません。そのため、騒音の予測計算は、対象とする音源からの音が背景騒音レベルを下回った時点で、実質的に意味をなさなくなります。

特に都市部のように広範囲に複数の音源が存在する環境では、状況はさらに複雑です。ある音源から離れると、今度は別の音源に近づくということが常に起こり得ます。したがって、ある地点の騒音レベルを正確に評価するには、影響を及ぼす複数の音源からの伝搬音をそれぞれ計算し、それらをエネルギー的に合成（総和）する必要があります。そもそも、その地域の背景騒音自体が、こうした無数の音源からの直接音や反射音が混じり合って形成されているのです。

また、高さ方向の変化にも注意が必要です。高層階に上がると、地上の建物などの障害物がなくなり見通しが良くなります。これにより、地上では遮られていた、より広範囲の多様な音源からの音が届くようになり、結果として地上よりも騒音レベルが上昇するケースも少なくありません。

特に、無数の音源がひしめく都心部では、地表面全体がひとつの巨大な面音源のように振る舞うと考えることができます。面音源の音は、そこから垂直方向に離れてもほとんど減衰しない特性があるため、都市部の高層階では「上にいくほど静かになる」という常識が通用しないのです。

まとめ

騒音の距離減衰は、基本的な考え方自体は単純なものの、周辺環境を考慮して考えた場合、複数の音源からの合成音の計算が必要になったり、反射音・回折音、背景騒音のレベルも考慮しなければならず、とても複雑な計算が必要になってきます。　また、計算精度を上げるためには、周辺環境の下調べはもちろん、実際に測定結果と比較して誤差の理由を検討したりしながら、計算精度を高めていく必要があります。

これまでの要点をまとめると

• 短辺の 1/3 までは面音源（距離減衰しない）
• 短辺の 1/3 以降で長辺の 1/3 までは線音源（倍距離 -3dB）
• 長辺の 1/3 以降は点音源（倍距離 -6dB）
• 距離減衰は背景騒音のレベルまで（背景騒音以下にはならない）
• 周辺の複数の音源からの総和を考える
• 高さ方向は距離が増すほど見通しが良くなり、かえってレベルが上昇する場合がある

今回は距離減衰の考え方について簡単にまとめてみました。

音の伝搬をイメージする際、私は音を光に例えるようにしています。点音源は「電球」、線音源は「蛍光灯」と考えるのです。そうすると、「どの場所が明るく、どこが暗いか」「この位置から見える光はどこから来ているのか」といった思考を応用できます。

このように考えると、「建物の陰でも反射した光でそこそこ明るい（反射音）」「ある地点は三方向からの光が重なり最も明るくなる（複数音源の合成）」といった状況が直感的に掴めます。　また、「光源が複数ある明るい環境では、一つの光源を消しても影響は限定的で、全体の明るさはさほど変わらない（特定音源の対策効果）」といったことも見通しやすくなります。

ちょっと変わった考え方かもしれませんが、音の伝搬についてイメージしやすくなりますので、ぜひお試しください。